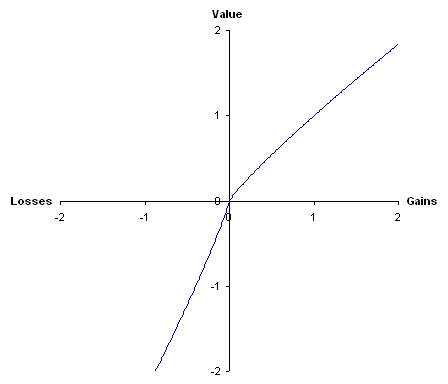
Figure 1: A hypothetical value function
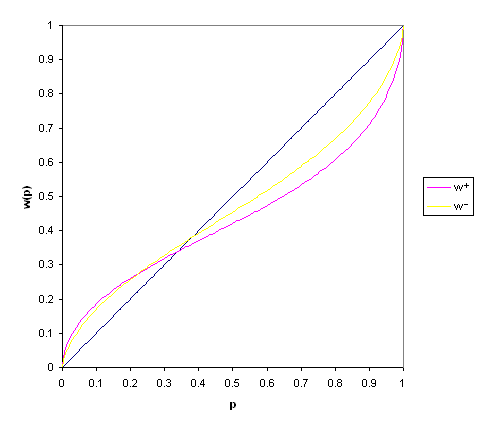
The most cited paper ever to appear in Econometrica, the prestigious academic journal of economics, was written by the two psychologists Kahneman and Tversky (1979). They present a critique of expected utility theory as a descriptive model of decision making under risk and develop an alternative model, which they call prospect theory. Kahneman and Tversky found empirically that people underweight outcomes that are merely probable in comparison with outcomes that are obtained with certainty; also that people generally discard components that are shared by all prospects under consideration. Under prospect theory, value is assigned to gains and losses rather than to final assets; also probabilities are replaced by decision weights. The value function is defined on deviations from a reference point and is normally concave for gains (implying risk aversion), commonly convex for losses (risk seeking) and is generally steeper for losses than for gains (loss aversion) (see Figure 1). Decision weights are generally lower than the corresponding probabilities, except in the range of low probabilities (see Figure 2).

There are two fundamental reasons why prospect theory (which calculates value) is inconsistent with expected utility theory. Firstly, whilst utility is necessarily linear in the probabilities, value is not. Secondly, whereas utility is dependent on final wealth, value is defined in terms of gains and losses (deviations from current wealth).
‘Kahneman & Tversky’s (1979) “Prospect Theory: An analysis of decision under risk” is the second most cited paper in economics during the period, 1975-2000 (Coupe, in press; Laibson & Zeckhauser, 1998).’
Wu, Zhang and Gonzalez (2004)
‘Prospect theory, developed in the early 1980s by the psychologists Daniel Kahneman and Amos Tversky, represents an important milestone in this context. Kahneman and Tversky proved in numerous experiments that the day-to-day reality of decision makers varies from the assumptions held by economists.’
Goldberg and von Nitzsch (2001, p. 12)
‘Prospect theory was developed by Kahneman and Tversky (1979). In its original form, it is concerned with behavior of decision makers who face a choice between two alternatives. The definition in the original text is: “Decision making under risk can be viewed as a choice between prospects or gambles." Decisions subject to risk are deemed to signify a choice between alternative actions, which are associated with particular probabilities (prospects) or gambles. The model was later elaborated and modified.’
Goldberg and von Nitzsch (2001, p. 62)
‘Prospect theory has probably done more to bring psychology into the heart of economic analysis than any other approach. Many economists still reach for the expected utility theory paradigm when dealing with problems, however, prospect theory has gained much ground in recent years, and now certainly occupies second place on the research agenda for even some mainstream economists. Unlike much psychology, prospect theory has a solid mathematical basis — making it comfortable for economists to play with. However, unlike expected utility theory which concerns itself with how decisions under uncertainty should be made (a prescriptive approach), prospect theory concerns itself with how decisions are actually made (a descriptive approach).
Prospect theory was created by two psychologists, Kahneman and Tversky, who wanted to build a parsimonious theory to fit a number of violations of classical rationality that they (and others) had uncovered in empirical work. Prospect theory bears more than a passing resemblance to expected utility theory.’
Montier (2002, p. 20)
Short description: ‘We have an irrational tendency to be less willing to gamble with profits than with losses..’
Tvede (1999, p. 94)
‘Prospect theory, which was developed by Kahneman and Tversky (1979), is one of the most often quoted and best-documented phenomena in economic psychology. The theory states that we have an irrational tendency to be less willing to gamble with profits than with losses.’
Tvede (1999, p. 166)
Prospect theory. We have an irrational tendency to be less willing to gamble with profits than with losses. This means selling quickly when we earn profits but not selling if we are running losses’
Tvede (1999, p. 169)
‘In their landmark work on prospect theory, a descriptive framework for the way people make choices in the face of risk and uncertainty...’
Shefrin (2000, p. 24)
‘...get-evenitis is central to prospect theory...’
Shefrin (2000, p. 108)
‘A theory that incorporates such framing effects has been proposed by Kahneman and Tversky (1979). Termed prospect theory, it has been extraordinarily influential. It is based on the idea that people evaluate gains or losses in prospect theory from some neutral or status quo point, an assumption consistent with the adaptation-level findings that occur not just in perception but in virtually all experience. That is, we adapt to a constant level of virtually any psychological dimension and find it to be neutral. In a similar way, we adapt to the reduced light in a movie theater when we enter it—finding it not particularly dark after a few seconds—and then readapt to the much brighter light outside when we leave the theater—finding it not to be unusually bright after a few seconds. But since choice varies by framing it as a gain or a loss, it cannot reveal underlying preferences.’
Dawes (2001, p. 195)
‘Not very long after expected utility theory was formulated by von Neumann and Morgenstern (1944) questions were raised about its value as a descriptive model (Allais, 1953). Recently Kahneman and Tversky (1979) have proposed an alternative descriptive model of economic behavior that they call prospect theory.’
Thaler (1980)
First, individuals do not assess risky gambles following the precepts of von Neumann-Morgenstern rationality. Rather, in assessing such gambles, people look not at the levels of final wealth they can attain but at gains and losses relative to some reference point, which may vary from situation to situation, and display loss aversion—a loss function that is steeper than a gain function. Such preferences—first described and modeled by Kahneman and Tversky (1979) in their ‘Prospect Theory’—are helpful for thinking about a number of problems in finance. One of them is the notorious reluctance of investors to sell stocks that lose value, which comes out of loss aversion (Odean 1998). Another is investors' aversion to holding stocks more generally, known as the equity premium puzzle (Mehra and Prescott 1985, Benartzi and Thaler 1995).’
Shleifer (2000, pp. 10–11)
‘If Richard Thaler's concept of mental accounting is one of two pillars upon which the whole of behavioral economics rests, then prospect theory is the other.’
Belsky and Gilovich (1999, p. 52)
‘...prospect theory deals with the way we frame decisions, the different ways we label—or code—outcomes, and how they affect our attitude toward risk. Indeed, we might just as easily have constructed this book as one long essay explaining prospect theory and all of the ideas that flow from it—that’s how influential and seminal the ideas discussed in Kahneman and Tversky's paper are.’
Belsky and Gilovich (1999, p. 52)
‘Prospect theory [...] helps explain how loss aversion, and an inability to ignore sunk costs, leads people to take actions that are not in their best interest. The sting of losing money, for example, often leads investors to pull money out of the stock market unwisely when prices dip.’
Belsky and Gilovich (1999)
‘In a nutshell, prospect theory assumes that investors' utility functions depend on changes in the value of their portfolios rather than the value of the portfolio. Put another way, utility comes from returns, not from the value of assets.’
Cornell (1999, p. 148)
‘Prospect theory was developed by Daniel Kahneman and Amos Tversky (1979), and it differs from expected utility theory in a number of important respects.
First, it replaces the notion of “utility” with “value.” Whereas utility is usually defined only in terms of net wealth, value is defined in terms of gains and losses (deviations from a reference point). Moreover, the value function for losses is different than the value function for gains. [...] the value function for losses (the curve lying below the horizontal axis) is convex and relatively steep. In contrast, the value function for gains (above the horizontal axis) is concave and not quite so steep. These differences lead to several noteworthy results.
Because the value function for losses is steeper than that for gains, losses “loom larger” than gains. For instance, a loss of $500 is felt more than a gain of $500.’
Plous (1993, p. 95–96)
‘Unlike expected utility theory, prospect theory predicts that preferences will depend on how a problem is framed. If the reference point is defined such that an outcome is viewed as a gain, then the resulting value function will be concave and decision makers will tend to be risk averse. On the other hand, if the reference point is defined such that an outcome is viewed as a loss, then the value function will be convex and decision makers will be risk seeking.’
Plous (1993, p. 97)
‘Prospect theory also differs from expected utility theory in the way it handles the probabilities attached to particular outcomes. Classical utility theory assumes that decision makers value a 50 percent chance of winning as exactly that: a 50 percent chance of winning. In contrast, prospect theory treats preferences as a function of “decision weights,” and it assumes that these weights do not always correspond to probabilities. Specifically, prospect theory postulates that decision weights tend to overweight small probabilities and underweight moderate and high probabilities.’
Plous (1993, p. 98)
‘Prospect theory represents a great improvement over classical expected utility theory. Indeed, many violations of expected utility theory are explicitly predicted by prospect theory.’
Plous (1993, p. 105)
‘The assumption of a diminishing marginal returns utility function relating dollar gains to utilities has been a cliché in economic theorizing and most reseach shows that our evaluations of gains show a negatively accelerating, diminishing returns pattern. In 1979, Daniel Kahneman and Amos Tvversky proposed what they termed prospect theory as a descriptive theory of decision behavior. A basic tenant of this theory is that the law of diminishing returns applies to good and bad quantitative consequences of decisions.’
Hastie and Dawes (2001, p. 216)
Hastie and Dawes (2001, p. 216)
‘The addition of a moveable reference level is the major difference between prospect theory and traditional economic utility theories.’
Hastie and Dawes (2001, p. 216)
‘v(x) = xα if x > 0
v(x) = -λ(-xα) if x < 0
(with a typical α = 0.88 and λ = 2.25)
This process has three major characteristics:
Hastie and Dawes (2001, p. 294)
‘Prospect theory is the best comprehensive description we can give of the decision process. It summarizes several centuries' worth of findings and insights concerning human decision behavior. Moreover, it has produced an unmatched yield of new insights and predictions of human behavior in decision making.’
Hastie and Dawes (2001, p. 310)
‘Some behaviors observed in economics, like the disposition effect or the reversing of risk aversion/risk seeking in case of gains or losses (termed the reflection effect), can be explained referring to the prospect theory.’
Articles published since 2000| 2001| 2002| 2003| 2004| 2005| 2006| 2007| 2008| 2009| 2010| 2011| 2012